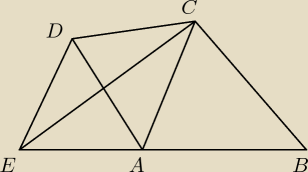
Geometria Sylwia: Na rysunku punkty E, A i B są współliniowe i odcinki DE i AC zawierają się w prostych równoległych. Uzasadnij, że pole czworokąta ABCD jest równe polu trójkąta EBC.

Sylwia: Podbijam, ruszy ktoś to zadanie?

Sylwia: już nie potrzebuje.

Kasia: Skoro masz rozwiązanie to pochwal się nim przyda się komuś innemu.

Jack: proste − nikomu się nie chciało pewnie pisać

Kasia: Mógłbyś to zrobić?

Jack: podziel na początek trójkąt EBC na EAC i ABC. Widać, że trójkąt ABC zawiera się również w czworokącie ABCD. Trzeba więc wykazać, że DAC (reszta czworokąta ABCD)=EAC (reszta trójkąta). Tak oczywiście jest − wynika to z własności trapezu, który mamy na wierzchołkach EACD. Mianowicie przekątne trapezu wyznaczają dwa trójkąty o równych polach (wspólna podstawa i taka sama wysokość).

Eta: https://matematykaszkolna.pl/forum/95659.html